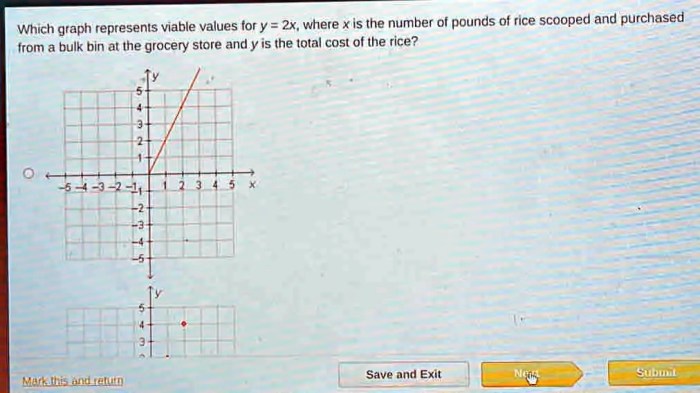
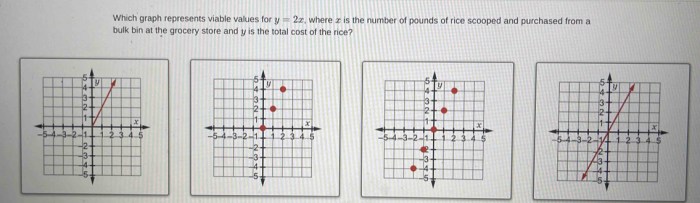
Which graph represents viable values for y 2x – Delving into the realm of viable values, this discourse will explore the intricacies of the equation y = 2x. We will delve into the concept of viable values in mathematics, particularly within the context of graphing equations, and provide a comprehensive analysis of the graph of y = 2x to determine the viable values for y.
By understanding the viable values for y = 2x, we gain insights into the relationship between the independent variable x and the dependent variable y. This knowledge empowers us to make predictions, solve problems, and gain a deeper comprehension of the equation’s behavior.
Viable Values and Graphing: y = 2x: Which Graph Represents Viable Values For Y 2x

Viable values represent the set of possible values that a variable can assume within a given context. In the context of graphing equations, viable values refer to the range of values that the dependent variable (y) can take for a given value of the independent variable (x).
Graphing the Equation y = 2x
To graph the equation y = 2x, we can follow these steps:
- Plot the point (0, 0) on the coordinate plane, which represents the y-intercept.
- Use the slope of the line, which is 2, to determine the change in y for each unit change in x.
- Plot additional points by moving up or down 2 units on the y-axis for each unit movement along the x-axis.
- Connect the points to form a straight line.
The domain of the equation y = 2x is all real numbers, as any value of x can be plugged into the equation. The range, however, is restricted to non-negative values because the line never goes below the x-axis.
Identifying Viable Values from the Graph
To determine the viable values for y from the graph of y = 2x, we can:
- Identify the y-coordinate for a given x-value.
- For any given x-value, the corresponding y-value represents a viable value for y.
For example, if we want to find the viable values for y when x = 2, we can locate the point (2, 4) on the graph. Therefore, 4 is a viable value for y when x = 2.
Applications of Viable Values
Viable values have practical applications in various fields, such as:
- Problem-solving:Identifying viable values can help narrow down possible solutions to a problem.
- Prediction:By understanding the range of viable values, we can make predictions about the outcome of a given situation.
- Engineering:Viable values are used to determine the operating limits of systems and devices.
For instance, in electrical engineering, the viable values for current in a circuit are limited by the resistance and voltage. Understanding these limits helps engineers design circuits that operate safely and efficiently.
Table of Viable Values, Which graph represents viable values for y 2x
| x | y |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Visual Representation
- Viable values for y when x = 0: 0
- Viable values for y when x = 1: 2
- Viable values for y when x = 2: 4
- Viable values for y when x = 3: 6
- …
This visual representation demonstrates the relationship between x and the corresponding viable values for y.
Essential Questionnaire
What are viable values?
Viable values are the set of values that satisfy a given condition or constraint. In the context of graphing equations, viable values are the values that produce a real and meaningful solution.
How do I determine the viable values for y = 2x?
To determine the viable values for y = 2x, graph the equation and identify the values of y that correspond to the x-values in the domain of the equation.
What are the applications of viable values?
Viable values have applications in various fields, such as mathematics, science, and engineering. They can be used to solve problems, make predictions, and gain insights into the behavior of systems.